The Map Is Not the Terrain

For instance, in looking at the typical Miller cylindrical projection map (below), it is hard to believe that Australia is actually about four times bigger than Greenland¹.

Figure 2 - Photo by Andrew Stutesman on Unsplash -                 

https://unsplash.com/photos/l68Z6eF2peA

Years later in college, I was really into discussing deep philosophical questions with my friend and housemate — followed by a lot of coffee (or beer, if it was Friday) — and eventually we heard about the Map Paradox (the name of which, I just found out, is actually Bonini's paradox²):  

“As a model of a complex system becomes more complete, it becomes less understandable.       Alternatively, as a model grows more realistic, it also becomes just as difficult to understand as the real-world processes it represents”.

It makes sense, right? I remember we discussed about how a map in which one mile in paper corresponds to one mile in real terrain is just not useful at all. On the other hand, a map in which one centimeter corresponds to one hundred thousand kilometers is not helpful either, if the goal is to find a market nearby (for more coffee!).

It is an important concept I try to keep in mind as an engineer and as a user of Computer Aided Engineering (CAE) programs. In order to make the design and analysis process productive, we are basically reducing a problem of enormous complexity, such as turbomachinery design and performance prediction, to models. And the map is not the actual territory³ (or, the model is not the physical thing itself).

So what? If maps and models are wrong, why use them at all?

Because, given the limitations and being aware of it, models help us to navigate in the real world. Basically, all models are wrong, but some are useful⁴.

Let’s say you are planning to go from point A to point B and your GPS application offers two routes: one takes one hour and another takes one-and-half hours. If you choose the first over the second, the actual ride may take longer than an hour. After all, the real road contains variables not predicted in the map (traffic, accidents, a strategic stop for a coffee). It is important to keep in mind that when map and terrain differ, follow the terrain⁵. But the time savings of roughly thirty minutes over the alternative route is real given the same circumstances. Therefore, this quick digital experiment using a model (two different routes in a GPS application) saves you time in the real world.

Figure 3 - Photo by Jean-Frederic Fortier on Unsplash

https://unsplash.com/photos/RkBTPqPEGDo

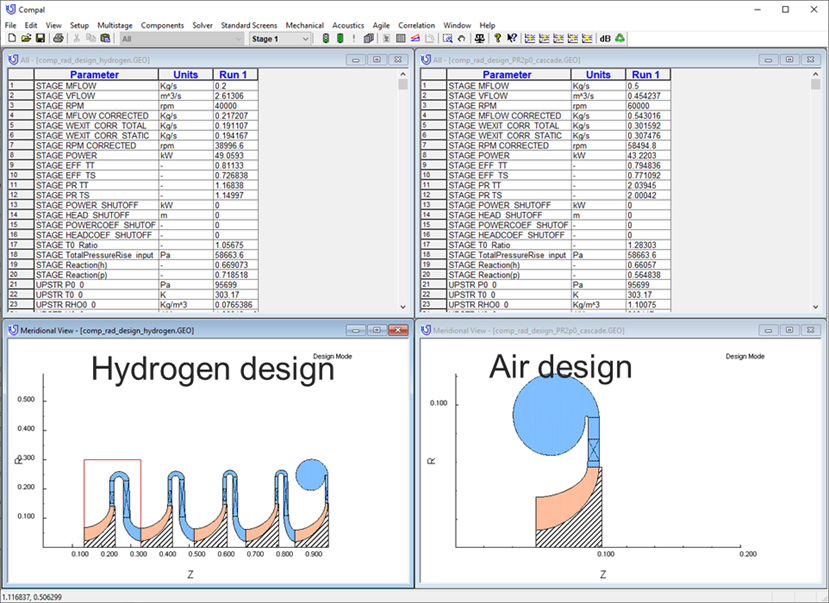
It is an analogous situation when an engineer runs a CFD (Computational Fluid Dynamics) simulation for a machine (let’s say the radial compressor in the picture below) and gets an efficiency of 78 percent. Let’s say the engineer works using his understanding of the CFD results, re-designs some of the machine parameters, runs another CFD simulation and now the performance is 83 percent. The actual efficiency in a test stand for this machine may not be 83 percent; there are too many variants taking place when manufacturing, assembling and operating the real machine. But the five percent efficiency improvement from one design to the second is real (given the same variables)!

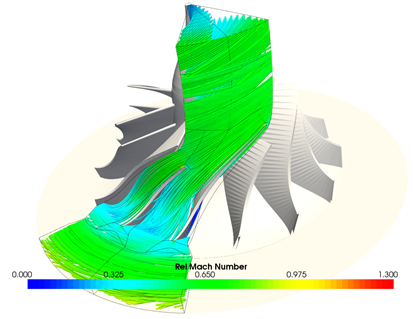
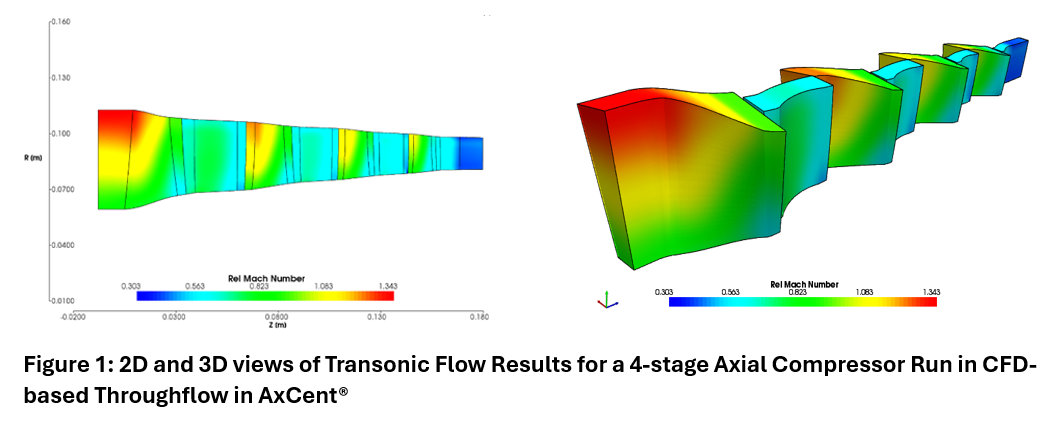
Figure 4 - A CFD simulation results displayed in our CAE program AxCent®

Now, let’s say we are designing a new compressor and for that we would use our longtime friend ideal gas equation (was this a nightmare for others in high school?) – Pv= RT – for the fluid definition. Using this equation could be fine if the fluid is air in ambient conditions. But for a refrigeration compressor in which the fluid is near the saturation line the equation will most likely underpredict your overall sizes and provide a non-realistic performance. In our CAE codes we have other fluid definitions available for that situation, such as our Peng-Robinson Cubic Equations (PRCE model for close friends) and the world famous REFPROP fluid libraries from NIST. As you grow in fidelity, though, the complexity also grows.

Every model is an abstraction and information that is lost makes the model manageable. The first step is to realize that you do not understand a model, map, or reduction unless you understand and respect its limitations⁵. In summary, real life is complex. But the moments of uncertainty can also be fun (comic below)! One must use the models wisely and consciously in order to make them not only practical but also reliable, whether in using your GPS for your weekend trip, your fluid models in our meanline codes or your turbulence models in CFD and the like.

Figure 5 - The moments of uncertainty are also my favorite !
(Credits: https://www.nathanwpyle.art/#/strangeplanet/ )

References:

1 -   https://www.mylifeelsewhere.com/country-size-comparison/australia/greenland#targetText=Australia%20is%20about%204%20times,is%20approximately%207%2C741%2C220%20sq%20km.

2 - https://en.wikipedia.org/wiki/Bonini%27s_paradox#cite_note-3

3 - http://esgs.free.fr/uk/art/sands-sup3.pdf

4 - https://www.sciencedirect.com/science/article/pii/B9780124381506500182?via%3Dihub

5 - https://fs.blog/2015/11/map-and-territory/