Entropy Happens… Deal with It!

If there’s one thing good about sitting in snarled traffic in Boston, it’s that you get to see some very original bumper stickers. The most recent bumper sticker I saw was probably the strangest one, no doubt created by some engineering professor who doesn’t see that the glass is half full, but that it has a safety factor of 2! Nevertheless, the bumper sticker stated the obvious when one thinks about it: ENTROPY HAPPENS! And then, to emphasize the point, the artist has the letters slowly “evaporating,” demonstrating graphically that entropy proceeds from order to chaos.

Yes, indeed, entropy does happen, and according to the Second Law of Thermodynamics, the entropy gain of the “universe” must be greater than zero. Ok, so it actually says that the entropy gain must be greater than OR EQUAL to zero; but we know that in the real world of engineering applications, we assume that entropy change in a process will always be greater than zero. 

So how can we deal with this universal truth? How can we use it to our advantage? Well, first, let’s be clear exactly what entropy is from an engineering point of view. Entropy change of a thermodynamic system is simply the measure of the heat transfer to or from a system, divided by the constant temperature at which that heat transfer occurs. The emphasis on the words “to or from” and “constant” is intentional, because it is necessary to keep track of the + or – direction of the heat transfer and only measure quantities of heat transfer that are transferred at a constant temperature, in absolute temperature units of Rankine (R) or Kelvin (K).

The concept of entropy was formulated by Sadi Carnot (1796-1832). He tried to explain why the First Law of Thermodynamics was simply not adequate in describing what everyone in the world observes: That a cold glass of water always get warmer when placed in an environment that is hotter than the original temperature of the water? The Conservation of Energy Law does not predict, nor disallow, that a cold glass of water can get colder when a quantity of heat is transferred from it. The Conservation of Energy Law simply states that the amount of energy taken out of the water must be accounted for as entering something else; that it cannot simply disappear. This is not to be confused with a corollary to the Second Law that indicates that exergy (yes…energy spelled with an “x”) does get destroyed - but that’s a subject for another hot, sunny day…pun intended!

If 100 BTUs of energy is removed from a glass of water at 60°F (520R), then it satisfies the First Law of Thermodynamics if that 100 BTUs of heat energy is used to heat the 80°F (540R) environment. The amount of entropy change for the cold glass of water will be measured as: -100 BTU/520R =-0.192 BTU/R and the amount of entropy change of the environment is measured as: +100/540= +0.185. The sum of these is the total entropy change = -0.007 Btu/R, which according to the Second Law, cannot happen because the total entropy change for a process must be greater than (or equal to) 0. 

What will happen is that the cold glass of water will receive 100 BTUs of heat energy from the warmer environment. For this energy exchange, the entropy change of the environment is -100/540= -0.185 and the entropy change of the cold glass of water (which gets warmer now) is: +100/520= 0.192, with the total entropy change equal to +0.007. 

It is not an exaggeration to say that from an Anthropic Principle point of view, humanity is saved by the Second Law of Thermodynamics because now, that cold glass of water will only be heated to the same temperature of the environment and not to an unbounded (think Big Bang Theory magnitude) temperature.

I think we can all agree that saving humanity is always a good thing, but now that we are here, engineers can also use the Second Law of Thermodynamics and the principle of “…total entropy change of the universe is always greater than zero” to perfect mechanical systems. Every mechanical device that produces or consumes power or exchanges heat and thus can be combined to make any and all known engineered systems, can be judged to be “as good as it can get” by measuring the total entropy change for each of the components. This may seem like an impossible task, but the task is made simpler by recalling that there are only seven basic devices that constitute all engineered systems: turbines, compressors, pumps, valves, nozzles, diffusers, and heat exchangers.

All these devices are critical to a well-engineered system, but perhaps where the application of the Second Law is most effective is in turbines, where power is produced, or in pumps and compressors, where power is consumed. Maximizing the power from turbines and minimizing the power for the pump and compressors can be accomplished by carefully looking at where entropy is produced within these components.

For example, in a professional development course once offered by Concepts NREC, the instructor presented the proper design of turbines and compressors to demonstrate how entropy production can be measured using Computational Fluid Dynamics (CFD). He used CFD to calculate the entropy change at its source: in the fluid that is undergoing expansion (in turbines) or compression (in pumps and compressors), when it is in poor contact with the surfaces of the blades that are expanding or compressing the fluid. 

The generation of unwanted vortices shown below are sources of entropy generation, and thus a degradation in the desired performance of these components. The properly designed blades as well as the contouring of the proper nozzle and diffuser blade shape are essential to reduce entropy generation, and thus increase the efficiency of the device. In the words of the course instructor: “…we do need estimates of the loss (entropy generation) … “in the continuous flow path of the fluid “…to connect one calculation to the next…” in a CFD analysis.

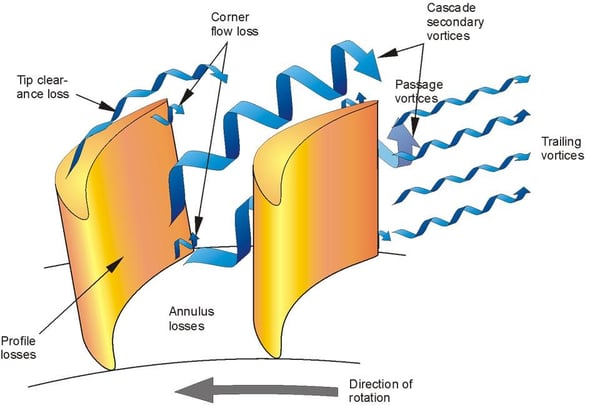
• Treat the turbine as a set of linked control volumes
• Use the 1D equations of mass, momentum, and energy to solve for conditions along a mean streamline at each station between C.V.s
• Assume conditions on the mean streamline represent passage-average conditions
• We don’t need to know what happens in each C.V., but we do need estimates of the loss (entropy generation), deviation (difference between flow angles and blade angles), and blockage in each to connect one calculation station to the next

That’s how Concepts NREC deals with the constraints of the Second Law of Thermodynamics when designing high-efficiency turbomachinery – we literally put entropy to work! Hey, that might make another good bumper sticker…