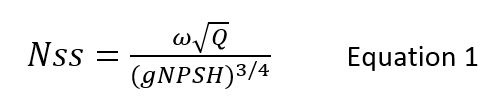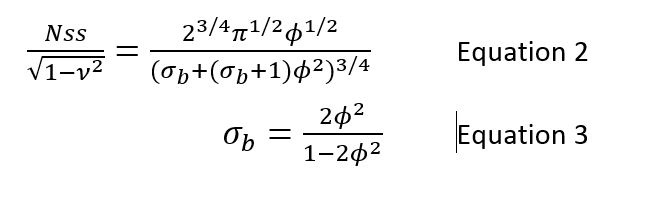How to Design a Pump for Reduced NPSH

Cavitation occurs in a pump when the bulk liquid pressure starts to approach the vapor pressure of the liquid, and cavities of vapor form as seen in Figure 1.  This figure shows the inlet of a cavitating pump tested in Concepts NREC’s water flow loop.  These cavities can degrade the head rise and efficiency of the pump, create instabilities, and cause significant damage to the pump impeller and other components.  To avoid these effects, a pump must operate with an inlet head that is at least as high as the required net positive suction head (NSPH) that the pump was designed to achieve.  The NPSH is the difference in the inlet head and the liquid vapor head (or vapor pressure converted to liquid head).  Many pumping systems would benefit from the ability to operate at lower NPSH and so reducing the required NPSH of a pump is often of great concern to pump designers.

Figure 1. View of the inlet of a cavitating pump that was tested in Concepts NREC’s laboratory

The so called Brumfield criteria provide a useful framework for understanding the flow physics of a pump’s NPSH.   Figure 2 shows a plot of the Brumfield criteria which is the theoretical maximum suction specific speed (Nss) that can be achieved for a given inlet flow coefficient.  Nss is defined in Equation 1 and combines the rotational speed (w), the flow rate (Q) and the net positive suction head (NPSH) into a non-dimensional parameter.  Suction specific speed allows for the comparison between different types of pumps because it accounts for the influence of rotational speed and flow rate on NPSH.  Higher values of Nss indicate better suction performance or lower NPSH.                       

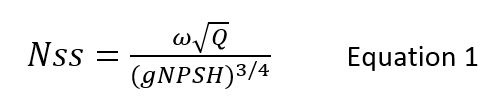
The Brumfield criteria can be derived by starting with the definitions of inlet flow coefficient (f), net positive suction head (NPSH), incompressible total pressure (P0), suction specific speed (Nss), blade cavitation coefficient (s_b), and inlet hub-to-tip radius ratio (n).   Using these definitions an alternate expression for suction specific speed as a function of s_b, f, and n is found (see Equation 2.)  The factor  in Equation 2 corrects the suction specific speed to take out the influence of the inlet hub radius from the results.  The term on the left hand side of Equation 2 is called the corrected suction specific speed.  Figure 2 shows curves of corrected Nss versus f for constant s_b.  For a given s_b there is a f that provides the maximum Nss value.  The locus of these maxima for varying f is termed the Brumfield criteria.  Equation 3 gives the optimum value of s_b for a given f and so the locus of maxima or the Brumfield criteria are found by combining Equations 2 and 3.                        

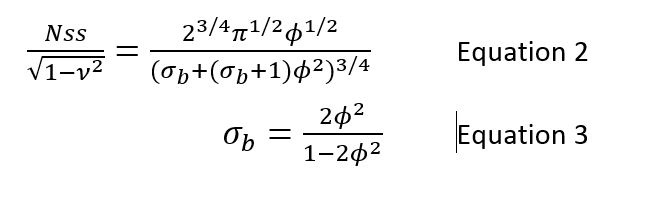
Notice that the Brumfield criteria do reasonably well at predicting Nss for f less than about 0.15.  However, the criteria under predicts the achievable levels of Nss for higher flow coefficients.   For pumps designed at high flow coefficients, the suction performance is often not the primary constraint for sizing the pump inlet.  In these cases the pumps could achieve higher suction performance by increasing the inlet eye size or flow coefficient, with the corresponding blade angle change; however, other constraints are often in play, such as efficiency or stable operating range, precluding a larger eye size.

Also note that the Brumfield criteria imply that a certain s_b must be achieved in order to obtain the desired Nss.  The blade cavitation coefficient (s_b) is the fraction of inlet relative kinetic energy that is involved in the local flow acceleration on the blades that leads to the formation of vapor cavities.  The value of s_b is primarily governed by the flow blockage due to the presence of the blades either from geometric or aerodynamic sources.  Therefore, a low value of s_b means thin blades and low flow turning.

From the above discussion, it is clear that flow coefficient is a primary factor that influences the Nss and therefore NPSH of a pump.  The selection of the proper inlet flow coefficient or eye size for the required NPSH is the first step in pump design. 

The next step is to think about the inlet tip blade angle and the flow incidence on the blade that can be tolerated over the operating range of the pump.  Some positive incidence will improve the suction performance since it increases the pressure rise of the flow as it comes on board  the blading and reduces the size of any cavity formation.  However, too much incidence will increase the amount of aerodynamic blockage and increase the amount of kinetic energy that goes towards cavitation.  High incidence also causes instabilities and reduced stable operating range.

The final step is to keep the thickness of the blades as small as possible near the inlet of the pump to minimize the amount of flow blockage introduced by the blades.  The higher the blade blockage, the more the available inlet kinetic energy goes towards cavitation and reduces the suction performance of the pump. 

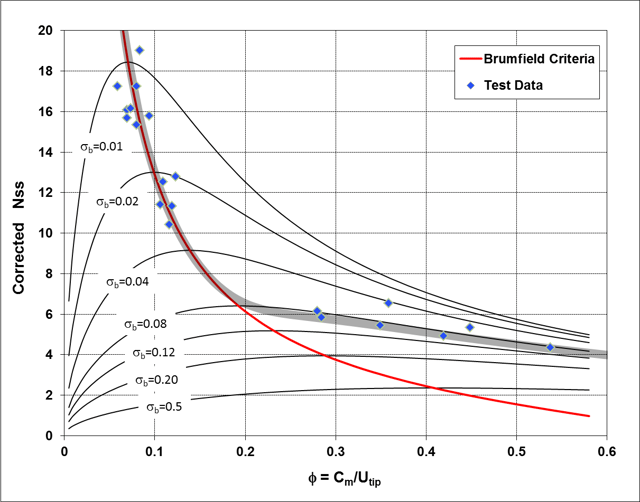
Figure 2.  Corrected suction specific speed (NSS) versus flow coefficient (f)

This is just a brief overview of the important factors that go into designing for low NPSH in a pump.  Flow coefficient, blade angle, and blade thickness are the primary parameters that influence the achievable level of NPSH.  Experience is required to know how to properly use these three parameters to design a pump for best NPSH. This is especially true over a wide flow range that meets all the other pump design goals such as efficiency, stability, and structural robustness.  Concepts NREC has many years of experience in research, design, analysis, and testing of low NPSH pumps. Contact us, we are here to help!