Ideally, the exit flow angle for an impeller should be the same as the exit blade metal angle. However, the exit flow angle deviates from the blade guidance at the impeller exit due to the finite number of blades. Correctly predicting flow deviation is a critical task in meanline and through-flow modeling because the exit flow angle is directly related to the work input and the pressure rise across the impeller.
For many years, engineers designing axial and radial turbomachines have applied completely different deviation or slip factor models. For axial applications, the most commonly used “deviation angle” model has been Carter’s rule or its derivatives. For radial centrifugal impellers, Wiesner’s “slip factor deviation” model correlation has been the most popular choice. But can these seemingly unrelated models be linked by a unified slip model for axial and radial impellers? This question becomes particularly important when designing a mixed-flow impeller where one has to choose between axial or radial slip models.
This slip model unifies the separate axial and radial models and is based on blade loading, or the velocity difference between the pressure and suction surfaces near the discharge of the impeller. The loading function includes the effect of blade rotation, blade turning, and the passage area variation. This velocity difference is then used to calculate the slip velocity using Stodola’s assumption. The model can be related to Carter’s rule for axial impellers and Stodola’s slip model for radial impellers.
To validate the model, a variety of different impellers were studied including radial compressors, axial compressors, pumps, and blowers. The sampling of cases presented here represents the typical results achieved.
Radial-compressor case studies and validation
Eckardt radial-compressor Rotor “O” and Rotor “A” were selected because detailed geometry definition at the impeller exit was available to properly set the blade-turning rate. The test data was reproduced from Eckardt’s original plots.
Both Wiesner’s correlation and this slip factor model did a good job matching the test data for Rotor “O.” However, the model was slightly on the low side while the Wiesner model was slightly high. Stodola’s model underpredicted the slip factor by a significant margin.
Test data showed a visible downward trend with the exit flow coefficient. This may have been indicating a slight positive flow turning near the discharge, resulting from the large wake region at the impeller exit. A better match was obtained when the blade-turning rate was set to 5.0m-1 (represented in the graph by a solid line). But to obtain this “better” match, the F factor had to be reduced from its default value to 0.65.
The Rotor “A” slip factor test data showed a distinctive upward trend with the increase of flow coefficient. Eckardt attributed his unusual trend to the S-shaped blade design of impeller A. Sturge and Cumptsy’s also confirmed this trend in their two-dimensional numerical simulation.
This slip model suggests that the flow coefficient at the impeller exit is an important variable for the slip factor when there is blade turning at the impeller discharge. This may explain the rise of the slip factor with flow coefficient. In order to compare it with Eckardt’s original plot, the European slip factor was plotted against the exit flow coefficient as shown.
According to this model, the slip factor is mainly affected by the impeller rotation on the radial plane and also blade turning when the blade-turning rate is significant at the impeller discharge. If the blade-turning effect is ignored, the slip factor model is similar to Stodola’s model. For many radial impellers, however, the blade-turning term is significant, and it is the key factor that controls the trend of slip factor variation.
Axial-compressor case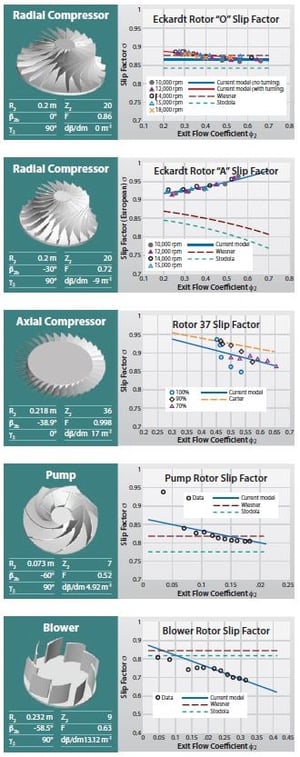
Both this model and Carter’s rule confirmed the test data that showed a linear decrease in the slip factor (because of the positive blade-turning rate) as the flow coefficient increased. These comparable results validated the potential for a unified radial and axial slip factor model to bridge the gap between their completely different approaches to deviation modeling. It also provides a potential model for cases with a mixed-flow exit.
Pump case
Because the viscosity of water is much greater than air, the friction force in the volute was probably responsible for reducing the impeller tangential velocity, thereby increasing the slip velocity and causing the slip factor to drop as the flow increased. Although the Wiesner model did not predict the downward trend with the flow coefficient, the slip factor prediction compared very closely with the test data. The Stodola model underpredicted the slip factor because it missed the F factor.
Blower case
The model matched the data well except for the points at low-flow coefficients. This may have been partially attributable to the recirculation loss model used during data processing. Both the Wiesner and Stodola models failed to predict the downward trend. Their predictions became worse when the flow coefficient increased.
Significance is considerable
The validation of this slip model provides sound explanations for the trends of slip factor variation with flow conditions and constitutes a consistent basis for calculating the slip factor of both axial and radial impellers. This not only fills a theoretical gap between radial and axial meanline modeling, it also allows direct application of the model to impellers with mixed-flow exits.
This model has identified the blade-turning rate at the impeller discharge as a key factor in the slip factor calculation. This parameter was hidden inside the axial deviation model through the camber angle and chord and completely missing from any existing slip factor models for radial impellers. The omission may be one of the reasons why a robust slip factor model has never been achieved.
The model confirms that a single-flow parameter, exit flow coefficient is correlated with the slip factor, and the slope of the correlation is determined by the blade-turning rate. The identification of this flow parameter may significantly influence future slip factor data processing and meanline modeling.
And finally, since the model is based on blade loading, which is a common factor for any rotor and stator in a turbomachinery application, it might possibly be applied to other areas, such as turbine rotors, radial diffusers, or inlet guide vanes.
A full paper was written on this subject GT2007-27064. Which was presented at ASME’s Turbo Expo.