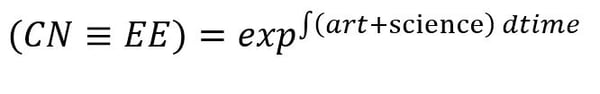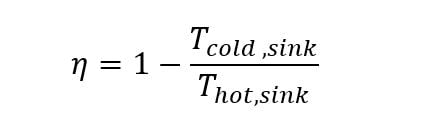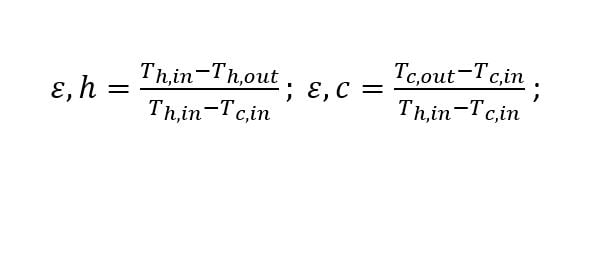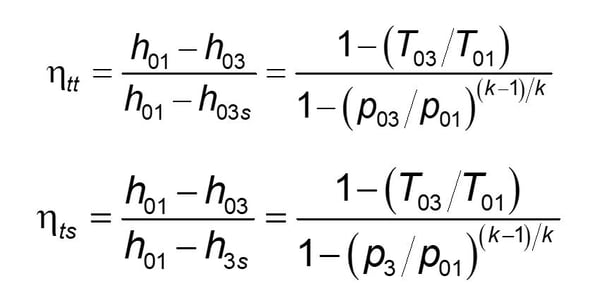Putting Entropy to Work

The previous blog, Entropy Happens… Deal with It! ended with the statement, “That’s how Concepts NREC deals with the constraints of the Second Law of Thermodynamics when designing high-efficiency turbomachinery – we literally put entropy to work!” That blog not only lead to an increase in sales of bumper sticker sales emblazoned with “Working on it, STAY TUNED!”, it led to a request to explore this statement in a little more detail – particularly as the idea might apply to the analysis, design and manufacturing of turbomachinery.

The earlier blog defined entropy in engineering terms, as opposed to philosophical terms, that simply exclaims that it is nature’s proclivity to proceed from order to chaos. The Second Law of Thermodynamics requires that the entropy change of the universe must always be equal to or greater than zero. We gave an example of why the Second Law of Thermodynamics was needed, but then also defined the universe as not being the stars and planets that fill the night sky, but a simple thermodynamic construct. It is a declaration that the calculation of engineering entropy must consider two “groups”: the collection of things that we call the system that is inside an imaginary boundary (traditionally called a Control Volume), but then also consider everything that is outside of that same control volume.

Basically, it is a recognition that the thermodynamic universe is complete when you account for how heat energy is exchanged between the only two things that make up the universe: the inside of something, and then everything else outside of the system of interest.

But how can engineers productively use an edict as given by the Second Law of Thermodynamics that entropy change of the universe will be greater than or equal to zero? Don’t the words “greater than” mean that the magnitude of entropy change can be any number greater than zero? Yes, that is clearly true. So how can engineers use the Second Law of Thermodynamics to improve the design of any system – let alone efficient turbomachinery – if entropy change can be limitless? The answer starts in antiquity with the often-maligned Alchemists. 

In many respects, the Alchemists of the Medieval Period and those that date as far back as 2,000 BC were the Edisons of the day, if only in the sense that they performed numerous experiments, mostly chemical in nature, to try to discover ways of making something of value from what was considered plentiful and useless in its original form. That’s perhaps an “entropy inspired” way of saying they tried to make gold from lead.

In fact, Alchemists used haphazard experimental methods without much basis in science and what Sir Francis Bacon later formulized as The Experimental Method. Alchemists tried something, and if it didn’t work, they tried something else. The one scientific principle that would have helped the ancient Alchemists was the ability to know if the experiment could work, and which ideas were a waste of valuable time.  

In today’s real-world of productive engineering endeavor, the Second Law of Thermodynamics provides that principle by using not the “greater than” part of the Second Law, but rather the “equal to” part of the Second Law. Consider a modern-day, brilliant, advance degreed engineer who knows everything about designing engines. In other words, a PhD student who graduated from a top university only last year.

This entrepreneur has an idea for an engine that burns food wastes that will have, according to the First Law of Thermodynamics, an engine efficiency of 75%. Calculations indicate that the food wastes can be ignited and burned in his Top Secrete Combustion system that is part of the Top, Top Secrete (sometimes written: Top²-Secrete) heat engine that achieves a combustion temperature of 1460 R (1000°F).

The entrepreneur works night and day and spares no expense to demonstrate that the claims for the high efficiency are valid. During one of many introspective moments between tests, an assistant brings the entrepreneur a small book entitled: “Reflections on the Motive Power of Heat” by Sadi Carnot (1884).  At home the night before, the assistant applied the one and only equation in the very short treatise to the specifications of the heat engine that is being tested. The simple and, someone would say, elegant equation for Carnot efficiency is:

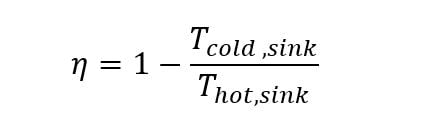
The text identifies this equation as derived from the Second Law of Thermodynamics “…when the entropy of the universe is set equal to minimum limit of zero (0)”.

The calculation reveals that the best possible efficiency for a heat source temperature of 1460 R and an ambient temperature of 520 R (60°F) is only 64%. Thus, the proposed efficiency of 75% is not possible per the Laws of Thermodynamics.  The assistant asks the entrepreneur to check his numbers, trying to understand why they have been trying to achieve an efficiency of 75% when this application of the Second Law of Thermodynamics indicates that the quest is futile.

By focusing on the identity part of the Second Law equation: ∆S _{“universe”} = 0 and not the inconclusive and thus less useful (but still true!) part of the Second Law:  ∆S _{“universe”} > 0, an engineer can at least identify the best possible outcome, given a set of engineering specifications.

From the point of view of saving engineering time and the expense of new product development, the more productive questions now become: How close can the proposed engineering system come to achieving this Holy Grail of engineering perfection defined by Carnot, and how can engineering principles and experience be used to approach this ideal solution?

All engineered systems are constructed of one or more of only seven primary mechanical machines:  turbine, compressor, pump, diffuser, nozzle, valve, and heat exchanger. These mechanical elements are manufactured with the intent of achieving as close to the Holy Grail of entropy change equal to zero as possible. The designers of heat exchanges can use the Second Law of Thermodynamics to define the “best possible heat exchanger performance” by using one of the two equations shown here:

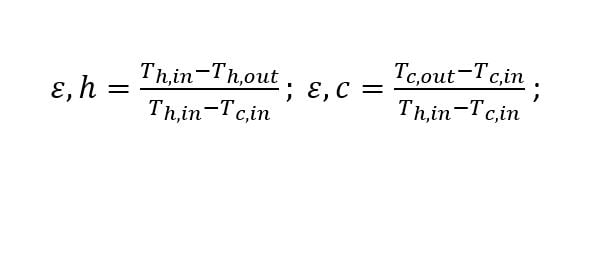These equations define the effectiveness of the heat exchanger and the maximum effectiveness for the heat exchanger is 100% only when the hot fluid exit temperature is cooled to be equal to the cold fluid’s inlet temperature OR when the cold fluid’s exit temperature can be heated to the hot fluid’s inlet temperature.  The reader is cautioned however that a 100% effective heat exchanger, similar to a 100% turbine or compressor is not possible.

Fortunately, achieving zero entropy change in the other five devices: the turbine, compressor, pump, nozzle and diffuser are what keep turbomachinery engineers busy. To gauge how close a new design comes to achieving the ideal performance, all manufacturers of these devices use a standard formula that compares the performance of the “real” device against the “ideal” device.  

For example, in designing a turbine, compressor, or pump, the enthalpy difference between the inlet of the device and the outlet is based on the enthalpy at the outlet of the device having the same fluid property of entropy at the exit as it has at the inlet. The fluid properties of entropy are tabulated for all fluids in handbooks or are available in several commercially available software programs. Using this standard protocol, manufacturers of turbines use an efficiency formula as shown here:

The denominator of this equation is often called the isentropic (i.e., constant entropy) enthalpy drop.  The pump and compressor efficiency equation are almost identical, with the only difference that the ratio is inversed to have the efficiency value always less than 1. Nozzle and diffuser efficiency equations are similar to the turbine efficiency and compressor efficiency equations, respectively.

An advancement in these equations is also commonly used in the detailed design of advanced turbomachinery that uses diffusers and nozzles as part of the turbine and/or compressor design. This leads to two efficiency terms for each of the components: a total-to-total (ηtt) efficiency and a total-to-static (ηts) efficiency term. The formulae are given here for ideal gasses:

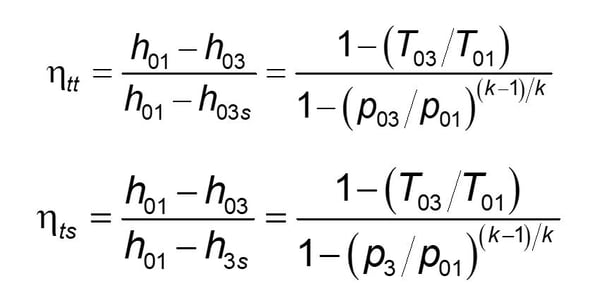
The Mollier diagram of h-s (below), is used to more clearly identify the different enthalpies used in these equations. Note that the denominators in these equations are different. The total-to-total efficiency will be higher by 1 or 2 pts in efficiency, compared to the total-to-static efficiency, because the fluid can be expanded to a higher pressure ratio if an exit diffuser is able to recover some of the kinetic energy in the fluid stream and produce higher pressure to match the turbine exit pipeline pressure.

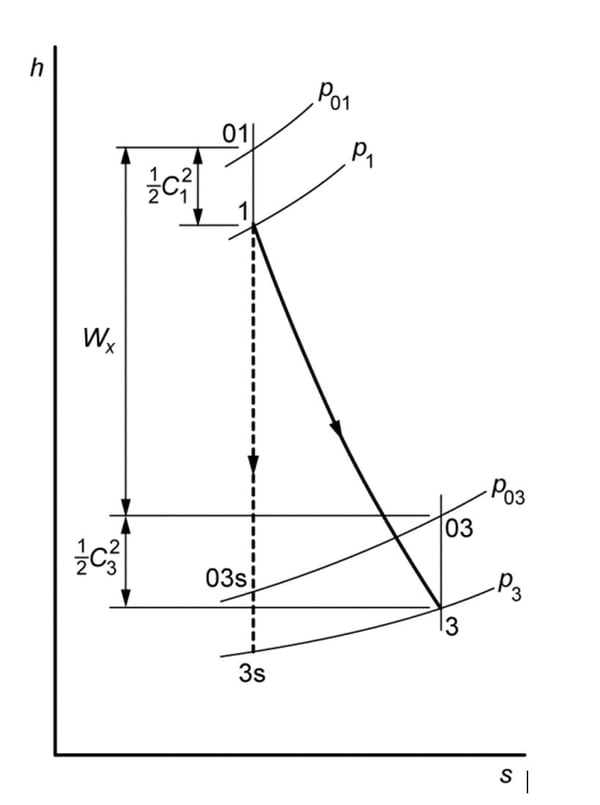
Clearly, the objective of a properly designed turbomachine is to have the efficiencies approach 1, and thus reduce the increase in entropy production in the fluid as it is expended (or compressed). To best accomplish this goal, it is best to have two distinct software programs in the hands of experienced engineers.

An experienced engineer working on an advanced design for a turbomachine must have software packages with the ability to seamlessly communicate the engineering design with the manufacturing of the impeller, in order to achieve the objective of “…putting entropy to work”. 

Concepts NREC’s suite of software for the design and manufacturing of turbomachines,  combined with Concepts NREC's Engineer’s tested experience does provide this integration of art and science – or in short: