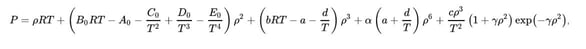The Gyroscopic Effect
This post covers one of the fundamental issues that makes rotordynamics a unique subject: The Gyroscopic Effect. The gyroscopic effect can be observed in the behavior of spinning tops, fidget...
Share
The Refprop program
The calculations in the National Institute of Standards and Technology (NIST) Refprop program are generally considered the most accurate thermo-fluid models available. The routines are widely used in many applications.
The models
Several different models are embedded in the Refprop formulation. The most important are the Benedict-Webb-Rubin equations of state for the pressure-temperature-density relationship.
The equation takes this form:
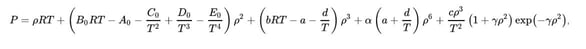
This is clearly way more complicated than the corresponding cubic implementation (Going Through a Phase – Modeling Phase Change with Cubics). Other equations get even more complex since many of these require various integrations and derivatives of this already complex equation.
Application
The Refprop calculations are considered to be the only formulation accurate enough to predict fluid properties near the difficult critical point. The plot, taken from Refprop itself (below), shows the critical point on a temperature vs. entropy plot (left) and z (compressibility) vs. pressure curve (right). The properties near the critical point are particularly nonlinear and change very rapidly, hence the challenge in calculating them.
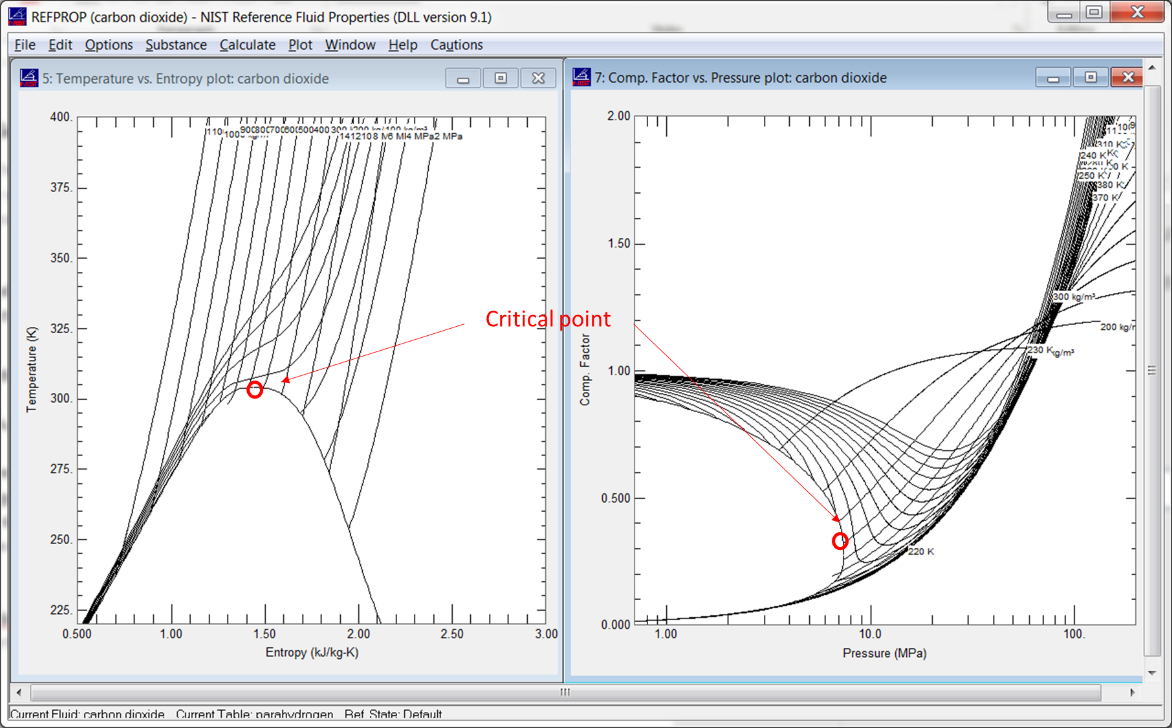
Encountering flow conditions near the critical point is actually quite rare. The high temperatures and pressures of most fluids at the critical point tend to be quite difficult to handle. New cycles which take advantage of fluid behavior near the critical point are actively being investigated though. Carbon dioxide, in particular, has attracted a lot of interest since its critical point is found at a reasonably low temperature.
The issues
As good as the Refprop calculations are, there are two important issues the user needs to consider when using it. The most important issue is the very slow run time. A CFD solver might make millions or possibly even billions of calls to the thermodynamic routines to the so-called equation of state (EOS) in the course of a solution. The computationally intensive Refprop calculation can eat up huge amounts of computational time in this situation. Several publications have documented CFD runtime increases more than 50 times when run with direct calls to Refprop. To get past this, most applications use a computational efficient interpolation scheme populated with NIST-derived data.
The second issue is that Refprop is quite unyielding outside its designated range. If a solver asks for something outside the tightly designed range limits, Refprop will refuse to answer. In programming terms, that means the dreaded NaN (not-a-number). While this could be considered an advantage, not to answer when outside the proper definition, it can be quite limiting. Many solvers iterate over a wide range of states before settling down to a more narrowly defined range. If any calls fail during any of these iterations, then the solution is done. This is true even if the solver might ultimately settle in a valid region after it stabilizes. Trapping these errors is necessary for all but the most stable and predictable iteration schemes.
Blogs in this series:
Fluid Phenomena Primer: Energy Versus Temperature, Specific Heat
Phase Change - Make Mine a Double!
When Perfect is Good Enough - Perfect Gas Models
What's Better than Perfect? Semi-Perfect Gas Models
Going Through a Phase – Modeling Phase Change with Cubics
