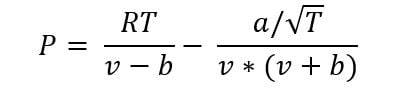The Gyroscopic Effect
This post covers one of the fundamental issues that makes rotordynamics a unique subject: The Gyroscopic Effect. The gyroscopic effect can be observed in the behavior of spinning tops, fidget...
Share
When fluids undergo a phase change (see Phase Change - Make Mine a Double), it typically has a very significant effect of the flow behavior and energy level of the system. Some examples of this are: cavitation in a pump, condensing near the exit of a steam turbine, even the everyday phenomenon of the weather is basically a never-ending phase change process of water, and its interaction with air.
Phase Change Example in Nature
The Cubic Models
To account for phase change in a thermo-fluid model, we need to take a big step up in complexity over the perfect gas (When Perfect is Good Enough – Perfect gas models) or even the semi-perfect gas model (What's Better than Perfect? Semi-Perfect Gas Models). Some of the most popular and efficient models are the so-called cubic equations of state.
The cubic model uses a two-part formula to express the pressure-density-temperature relationship. The formula for the Redlich–Kwong model is expressed as:
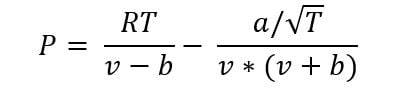
The first term is very similar to the perfect gas equation and is functionally equivalent when the value of v is much higher than b, which it usually is for a gas. The second term, sometimes called the “attractive term”, becomes dominant closer to the liquid phase. The attractive term represents the actual attraction/repulsion between molecules when the distance between them is no longer large compared to the molecule size.
The Implementation
There’s actually more to the cubic equation than just the formula above. The “cubic” in the cubic equation is a result of the fact that there are 3 possible solutions to the equation. In other words, there are 3 values of v that can potentially give the same p. To determine which one is valid requires some additional calculations.
The two dominant cubic models are the Peng-Robinson and the Redlich–Kwong models. They’re similar in that they are both cubic in nature, but the formula differs a bit between them.
The benefit of a cubic model is that it can model the phase change and capture the high variation in energy and volume that phase change entails. It possible to implement these models with only a minimal set of fluid data, namely, the critical pressure, critical temperature, and an “eccentricity factor”. The eccentricity is a measure of the deviation of the molecular shape from spherical.
The downside of the cubic equations is that they take more computational overhead than the simple perfect gas, semi-perfect gas, or simple incompressible liquid models. One can expect a modest degradation in runtime in CFD, or other flow models, with a cubic model, but this is usually acceptable.
The cubic models are considered very accurate in the gas phase and partial liquid phase, but less so for pure liquids, or around the critical point. The critical point is where the fluid exhibits both liquid and gas behavior, and the energy of the phase change approaches zero. Hundreds of variations of these cubic models have been proposed to address these limits. These have had some real successes in improving prediction in certain regions, but not universally.
The cubic equation applies only to the pressure-density-temperature relationship. The energy equation is usually solved with a semi-perfect representation. The cubic models work very nicely near the gas phase boundary and with moderate amounts of liquid present. As such, they are very functional for typical applications of fluids like natural gas, steam, and refrigerants. Refrigerants are used primarily in the gas phase, but near the saturation line, which show non-perfect gas-like behavior.
Wrapping Up
To model proprieties near the critical point, generally a more involved model is required for very high accuracy. These are rare applications in turbomachinery but some specialized designs do require this. This will be a topic in another blog (Getting Real – Advanced Real Gas Models).
Blogs in this series:
Fluid Phenomena Primer: Energy Versus Temperature, Specific Heat
Phase Change - Make Mine a Double!
When Perfect is Good Enough - Perfect Gas Models
What's Better than Perfect? Semi-Perfect Gas Models
Going Through a Phase – Modeling Phase Change with Cubics
