What's Better than Perfect? Semi-Perfect Gas Models

In a previous blog, Fluid Phenomena Primer: Energy Versus Temperature, Specific Heat, I explained the behavior for gas phase fluids and how the temperature is affected at high energy levels.  In another blog, When Perfect is Good Enough - Perfect Gas Models, we looked at the simple perfect gas model.  In this blog, we’ll explore the next step up in the hierarchy of gas thermodynamic modeling: semi-perfect gas.

What is a semi-perfect gas?

A semi-perfect gas model is one where the ideal gas law is followed:

            Pressure = Density * Gas Constant *Temperature

but the energy calculation is more complicated:

            Enthalpy =  ∫ Specific Heat * dT

Where the specific heat is no longer constant.

The model…

To solve this equation, we need some representation of the specific heat (Cp) as a function of temperature.  Many options are possible, but the most common form usually looks something like this:

            Cp = a + b*T + c*T² + d*T³+ e*T⁴

Again, many variations are possible, but this form is the most common.  The constants in the equation (a, b, c, d, e) must be taken from empirical data for the particular fluid, as there is no universal expression for these terms. 

Integrating the formula from above gives the equation for energy (enthalpy):

H = a*T + b*T²/2 + c*T³/3 + d* T⁴/4+ e* T⁵/5

The entire approach is non-iterative and very fast.  Although it's slightly more complicated than the perfect gas formulation, the extra computational overhead of a semi-perfect gas model is usually small.

The Caveat…

There is one caveat to the semi-perfect gas model that needs to be avoided at all costs: running off the range of the model.

The polynomial curves are fitted to a specific range and beyond that, range is an extreme danger zone.  The simple example below shows the point.  In red is a plot of specific heat for oxygen, taken from a formula (similar to the one above) from the back of the text The Properties of Gases and Liquids, 5^th Edition.  In black is the more accurate data from a more rigorous formulation from NIST’s Refprop program. 

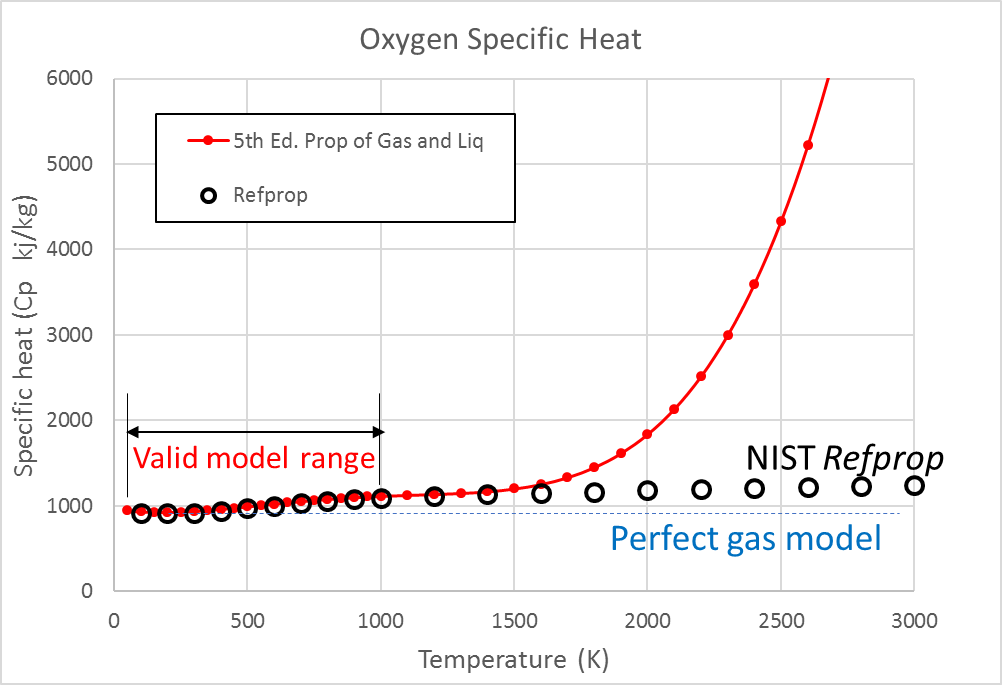
Note the polynomial model in red does a fine job in the recommended range but is terrible at higher temperatures.  Any attempt to use the model in this high temperature region would produce way more error than even the simple perfect gas model, shown in blue.  Carelessly going out of range will introduce a first order error, trying to correct for what is only a second order effect to begin with. 

Wrapping up….

So, thinking out of the box is something you should not do for semi-perfect gas modeling.  If you stay within the lines, the model will work quickly and stably, for almost all applications.  For compressors at moderate pressure ratios and temperatures, it's usually fine to use a semi-perfect gas model.  Turbines, which tend to run hotter, are also usually fine, provided the temperature limit is not exceeded. 

All this is predicated on the assumption that everything is in gas phase.  If there’s a phase change, which is common in a steam turbine, then a fancier model must be used, and I'll cover that in another blog.

Blogs in this series:

Fluid Phenomena Primer: Energy Versus Temperature, Specific Heat

Phase Change - Make Mine a Double!

When Perfect is Good Enough - Perfect Gas Models

What's Better than Perfect? Semi-Perfect Gas Models

Going Through a Phase – Modeling Phase Change with Cubics

Getting Real – Advanced Real Gas Models

Fluid Modeling: Liquified

The Ultimate Fluid Model: Non-Equilibrium Modeling