When Perfect is Good Enough - Perfect Gas Models

What is a perfect gas?

A perfect gas is one that has a linear variation in energy with respect to temperature and a linear variation in pressure with respect to temperature at constant volume. The perfect gas model is the simplest of all models for gas phase fluids. For a perfect gas, we need only two unique properties of the substance to determine the relationships between pressure, density, energy, and temperature. 

The most commonly used properties are the specific heat (Fluid Phenomena: Energy versus Temperature, specific heat) and the gas constant. Specific heat determines the change in energy with respect to temperature; the gas constant determines the relationship between pressure, density, and temperature. Alternatives like the molecular weight and ratio of specific heats can also be used as these can be derived from the specific heat and gas constant or vice versa.

The model

Perfect gases obey the ideal gas law stated as:

              Pressure = density * Gas constant *temperature

The second equation for energy is:

              Enthalpy = specific heat *temperature

Note enthalpy is a basic measure of energy. That’s it. It's very simple to understand and very simple to program.

We may or may not be interested in secondary variables like viscosity, surface tension, or thermal conductivity and there are separate models for these, mostly empirical. Other qualities like speed of sound and internal energy can be derived directly from the above equations.

What’s real and what’s not

People often talk about this or that fluid being a “perfect” or a “real” gas, but this is a misnomer.  Any gas can exhibit perfect or non-perfect (i.e., “real”) behavior depending on the temperature and pressure levels. Generally, as gas approaches a phase change, it starts to deviate from perfect gas behavior. Also, at high temperature, the energy versus temperature relation becomes variable and therefore less perfect.

A variation on the ideal gas law can be expressed as:

              Pressure = density * z *Gas constant *temperature

Where “z” is referred to as the “compressibility factor”.  In a nut shell, when z equals 1.0, then we have a perfect gas.  So, the measure of how good the perfect gas assumption is, is a direct function of z. 

The figures below show the value of z for two different fluids at various pressures and temperatures. The fluid on the left is the refrigerant, R32, widely considered a “real” gas. On the right is argon, widely considered a perfect gas. Not so different, are they? Both show regions where the gas behaves perfectly (z~1) and regions where it's way off. The difference is that the behavior of argon is more perfect at common pressures and temperatures. Refrigerants, in contrast, are used most often near the saturation line where the real behavior is strongest. 

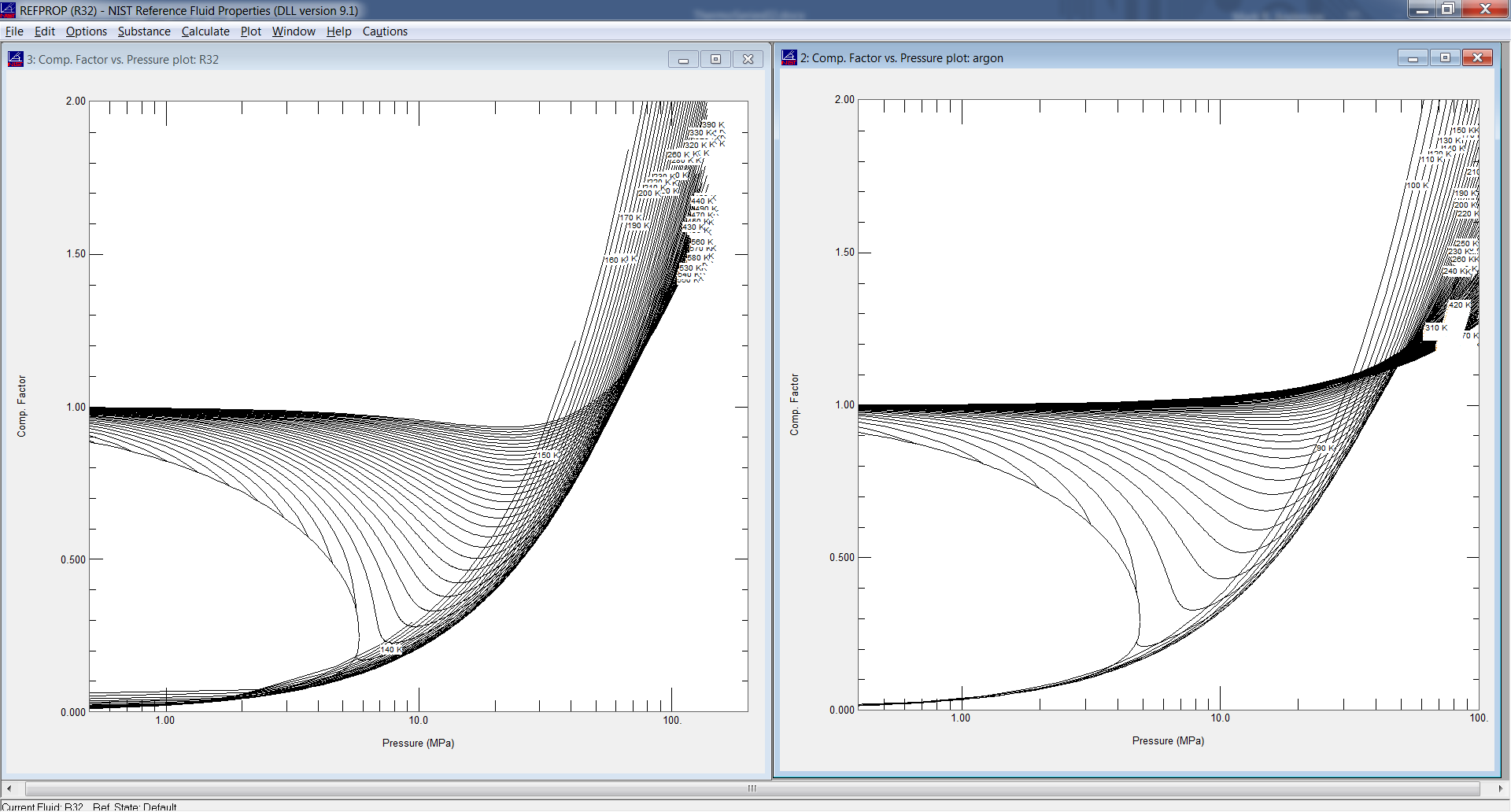
As the plots clearly show, gases tend to behave most like perfect gases at low pressures and at low temperature, provided they are not too close to the phase boundary.  

Nearly perfect

One trick to improve accuracy is to use the perfect gas model more locally. In other words, use a value of specific heat and gas constant relevant to the pressure and temperature you’re interested in. As long as you don’t drift too far in range, the model will be good. Those numbers in the back of your thermodynamic text are certainly for a state near room temperature and pressure.  Those could be far off from the region you're interested in. 

Wrapping up

Most fluid solvers provide a variety of different thermodynamic models for the user. The perfect gas model is just about guaranteed to be the fastest and most stable. Whether or not it's accurate enough depends on the local conditions and range of interest. My experience is that people tend to exaggerate the effects of real gas behavior, but that said, it can be very, well… real.

Blogs in this series:

Fluid Phenomena Primer: Energy Versus Temperature, Specific Heat

Phase Change - Make Mine a Double!

When Perfect is Good Enough - Perfect Gas Models

What's Better than Perfect? Semi-Perfect Gas Models

Going Through a Phase – Modeling Phase Change with Cubics

Getting Real – Advanced Real Gas Models

Fluid Modeling: Liquified

The Ultimate Fluid Model: Non-Equilibrium Modeling